Vahşi Güvercinler

Geçtiğimiz hafta, bir eşkenar üçgeni örtmek için en azından kaç tane daha küçük eşkenar üçgene ihtiyaç olduğunu kendimize sorduk. Bu daha küçük üçgenler eşit olmak zorunda değildir ve üst üste gelebilirler. Cevap 3'tür ve buna en küçük olasılığı hariç tutarak ulaşırız: 3 ile açıkça mümkündür ve 2 ile mümkün olmadığını göstermek (nasıl?) zor değildir.

Eşkenar üçgenin 5 noktası problemine ilişkin olarak çeşitli yaklaşımlar önerilmiştir; ancak en "sınırlı" olanı Francisco Montesinos'un yaklaşımıdır:

"Orijinal eşkenar üçgenin kenarlarının orta noktalarını birleştirerek, kenarları 1/2 m olan 4 eşkenar üçgen elde ederiz. Verilen 5 noktadan ikisi, indirgenmiş olanların aynı üçgeni içinde olacaktır, bu yüzden mesafeleri d, d>1/2 olamaz."

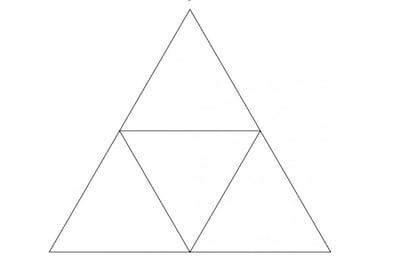
Gerçekten de, başlangıç ​​üçgenini 4 eşit üçgene bölerek, her biri 5 güvercin veya nokta barındırması gereken 4 boşluklu bir güvercinlik yaratılır. Ve kenar uzunluğu 1/2 m olan bir eşkenar üçgende var olabilecek en büyük mesafe tam olarak kenarın uzunluğudur, bu nedenle içinde bulunan herhangi iki nokta en fazla 1/2 m aralıklı olabilir (ve açıkça üçgenin köşeleridir).

Rafael Granero'nun çözümü biraz daha karmaşıktır , ancak daha az ilgi çekici değildir:

“Elbette, en uzak olması gereken dört nokta vardır ve hatta dört nokta verildiğinde, bunların birbirlerinden olabilecekleri en uzak nokta olduğu bile söylenebilir: üç köşe ve merkez. Merkez, üç köşeden herhangi birine 57,7 cm uzaklıktadır. Merkezde bulunan noktanın ne kadar küçük olursa olsun herhangi bir hareketi, kaçınılmaz olarak bir veya iki köşeye olan mesafeyi azaltacaktır. Ve aynı şey, köşelerde bulunan noktaların her biri için diğer üç noktaya göre geçerlidir. Merkez noktasından 50 cm'den daha fazla uzaklıkta olan tek noktalar, eşkenar üçgenin merkezinde merkezlenmiş, yarıçapı 50 olan bir dairenin dışındaki noktalardır. Ancak üç bölgenin her birinde, tüm noktalar en uzak noktadan, yani köşeden 8 cm'den daha azdır, bu nedenle diğer dört noktadan 50 cm'den daha fazla uzaklıkta olan beşinci bir nokta bulmanın bir yolu yoktur.”

Sanki laf arasında, 3 eşit sayı elde etmek için zarı 13 kez atmanın ne kadar düşük bir ihtimal olduğu sorulmuş ve Juan Zubieta'nın cevabı şu olmuş:

"13. zar atma olasılığı, 6 çift sayının (12!/2^6) olası permütasyonlarının ve tüm olası zar atma dizilerinin (6^12) bölümüdür. Sonuç: 1925/559872 (yaklaşık 291'de bir şans)." (Unutmayın, 3 kez 6 gibi belirli bir sayıyı elde etmekle ilgili değil, en az 3 kez bir sayının gelmesiyle ilgilidir.)

Yüksek riskli güvercinlik

Son birkaç haftadır verilen eğitimlerden sonra, özellikle güvercin yuvası ilkesinin yalnızca en basit sorunlara uygulanabilen bir gerçek olduğunu düşünenlere adanmış, Paul Erdös'ün dikkatini çeken bir klasik:

{1, 2, …, 2n} kümesi verildiğinde, n+1 sayının herhangi bir alt kümesinde, biri diğerinin katı olan en az iki sayı bulunacağını gösterin.

En sıcak saatlerde çözmeye çalışmayın: Bu yüksek riskli kümesteki güvercinler beyin hücrelerinizi yakabilir.